Intrusive non balanced binary tree container. More...
#include <bintree.h>
Classes | |
| struct | Node |
| Binary tree node. More... | |
Public Types | |
| typedef T | value_type |
| typedef TCompare | value_compare |
| typedef value_type & | reference |
| typedef const value_type & | const_reference |
| typedef value_type * | pointer |
| typedef const value_type * | const_pointer |
| typedef ptrdiff_t | difference_type |
| typedef size_t | size_type |
| typedef BinTreeIterator< BinTree< T, TCompare >, T > | iterator |
| typedef BinTreeConstIterator< BinTree< T, TCompare >, T > | const_iterator |
| typedef BinTreeReverseIterator< BinTree< T, TCompare >, T > | reverse_iterator |
| typedef BinTreeConstReverseIterator< BinTree< T, TCompare >, T > | const_reverse_iterator |
Public Member Functions | |
| BinTree (const TCompare &compare=TCompare()) noexcept | |
| template<class InputIterator > | |
| BinTree (InputIterator first, InputIterator last, const TCompare &compare=TCompare()) noexcept | |
| BinTree (const BinTree &) noexcept=default | |
| BinTree (BinTree &&) noexcept=default | |
| ~BinTree () noexcept=default | |
| BinTree & | operator= (const BinTree &) noexcept=default |
| BinTree & | operator= (BinTree &&) noexcept=default |
| operator bool () const noexcept | |
| Check if the binary tree is not empty. | |
| bool | empty () const noexcept |
| Is the binary tree empty? | |
| size_t | size () const noexcept |
| Get the binary tree size. | |
| T * | root () noexcept |
| Get the root binary tree item. | |
| const T * | root () const noexcept |
| T * | lowest () noexcept |
| Get the lowest binary tree item. | |
| const T * | lowest () const noexcept |
| T * | highest () noexcept |
| Get the highest binary tree item. | |
| const T * | highest () const noexcept |
| bool | compare (const T &item1, const T &item2) const noexcept |
| Compare two items: if the first item is less than the second one? | |
| iterator | begin () noexcept |
| Get the begin binary tree iterator. | |
| const_iterator | begin () const noexcept |
| const_iterator | cbegin () const noexcept |
| iterator | end () noexcept |
| Get the end binary tree iterator. | |
| const_iterator | end () const noexcept |
| const_iterator | cend () const noexcept |
| reverse_iterator | rbegin () noexcept |
| Get the reverse begin binary tree iterator. | |
| const_reverse_iterator | rbegin () const noexcept |
| const_reverse_iterator | crbegin () const noexcept |
| reverse_iterator | rend () noexcept |
| Get the reverse end binary tree iterator. | |
| const_reverse_iterator | rend () const noexcept |
| const_reverse_iterator | crend () const noexcept |
| iterator | find (const T &item) noexcept |
| Find the iterator which points to the first equal item in the binary tree or return end iterator. | |
| const_iterator | find (const T &item) const noexcept |
| iterator | lower_bound (const T &item) noexcept |
| Find the iterator which points to the first item that not less than the given item in the binary tree or return end iterator. | |
| const_iterator | lower_bound (const T &item) const noexcept |
| iterator | upper_bound (const T &item) noexcept |
| Find the iterator which points to the first item that greater than the given item in the binary tree or return end iterator. | |
| const_iterator | upper_bound (const T &item) const noexcept |
| std::pair< iterator, bool > | insert (T &item) noexcept |
| Insert a new item into the binary tree. | |
| std::pair< iterator, bool > | insert (const const_iterator &position, T &item) noexcept |
| Insert a new item into the binary tree with a position hint. | |
| T * | erase (const T &item) noexcept |
| Erase the given item from the binary tree. | |
| iterator | erase (const iterator &it) noexcept |
| Erase the given item from the binary tree. | |
| void | clear () noexcept |
| Clear the binary tree. | |
| void | swap (BinTree &bintree) noexcept |
| Swap two instances. | |
Friends | |
| template<typename U , typename UCompare > | |
| void | swap (BinTree< U, UCompare > &bintree1, BinTree< U, UCompare > &bintree2) noexcept |
Detailed Description
class CppCommon::BinTree< T, TCompare >
Intrusive non balanced binary tree container.
Binary trees are the good structures for associative searching. They keep items in sort order, so each of item can be found in a short time.
Not thread-safe.
Overview
In computer science, a binary search tree (BST) is a binary tree which has the following properties:
- Each node has a value.
- A total order is defined on these values.
- The left subtree of a node contains only values less than or equal to the node's value.
- The right subtree of a node contains only values greater than or equal to the node's value.
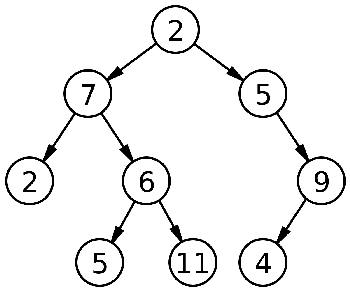
The major advantage of binary search trees is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient.
Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays.
If a BST allows duplicate values, then it represents a multiset. This kind of tree uses non-strict inequalities. Everything in the left subtree of a node is strictly less than the value of the node, but everything in the right subtree is either greater than or equal to the value of the node.
If a BST does not allow duplicate values, then the tree represents a set with unique values, like the mathematical set. Trees without duplicate values use strict inequalities, meaning that the left subtree of a node only contains nodes with values that are less than the value of the node, and the right subtree only contains values that are greater.
The choice of storing equal values in the right subtree only is arbitrary; the left would work just as well. One can also permit non-strict equality in both sides. This allows a tree containing many duplicate values to be balanced better, but it makes searching more complex.
Most operations on a binary search tree take time directly proportional to the tree's height, so it is desirable to keep the height small. Ordinary binary search trees have the primary disadvantage that they can attain very large heights in rather ordinary situations, such as when the keys are inserted in order. The result is a data structure similar to a linked list, making all operations on the tree expensive. If we know all the data ahead of time, we can keep the height small on average by adding values in a random order, but we do not always have this luxury, particularly in online algorithms.
Self-balancing binary trees solve this problem by performing transformations on the tree (such as tree rotations) at key times, in order to reduce the height. Although a certain overhead is involved, it is justified in the long run by drastically decreasing the time of later operations.
The height must always be at least the ceiling of log n, since there are at most 2k nodes on the kth level; a complete or full binary tree has exactly this many levels. Balanced BSTs are not always so precisely balanced, since it can be expensive to keep a tree at minimum height at all times; instead, they keep the height within a constant factor of this lower bound.
Times for various operations in terms of number of nodes in the tree n:
- Lookup - O(log n)
- Insertion - O(log n)
- Removal - O(log n)
- In-order iteration over all elements - O(n)
For some implementations these times are worst-case, while for others they are amortized.
Applications
Self-balancing binary search trees can be used in a natural way to construct associative arrays; key-value pairs are simply inserted with an ordering based on the key alone. In this capacity, self-balancing BSTs have a number of advantages and disadvantages over their main competitor, hash tables. Lookup is somewhat complicated in the case where the same key can be used multiple times.
Many algorithms can exploit self-balancing BSTs to achieve good worst- case bounds with very little effort. For example, if binary tree sort is done with a BST, we have a very simple-to-describe yet asymptotically optimal O(n log n) sorting algorithm (although such an algorithm has practical disadvantages due to bad cache behavior). Similarly, many algorithms in computational geometry exploit variations on self- balancing BSTs to solve problems such as the line segment intersection problem and the point location problem efficiently.
Self-balancing BSTs are a flexible data structure, in that it's easy to extend them to efficiently record additional information or perform new operations. For example, one can record the number of nodes in each subtree having a certain property, allowing one to count the number of nodes in a certain key range with that property in O(log n) time. These extensions can be used, for example, to optimize database queries or other list-processing algorithms.
References
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 6.2.3: Balanced Trees, pp.458-481.
Taken from:
Binary search tree from Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/Binary_search_tree
- Examples
- containers_bintree.cpp.
Member Typedef Documentation
◆ const_iterator
| typedef BinTreeConstIterator<BinTree<T, TCompare>, T> CppCommon::BinTree< T, TCompare >::const_iterator |
◆ const_pointer
| typedef const value_type* CppCommon::BinTree< T, TCompare >::const_pointer |
◆ const_reference
| typedef const value_type& CppCommon::BinTree< T, TCompare >::const_reference |
◆ const_reverse_iterator
| typedef BinTreeConstReverseIterator<BinTree<T, TCompare>, T> CppCommon::BinTree< T, TCompare >::const_reverse_iterator |
◆ difference_type
| typedef ptrdiff_t CppCommon::BinTree< T, TCompare >::difference_type |
◆ iterator
| typedef BinTreeIterator<BinTree<T, TCompare>, T> CppCommon::BinTree< T, TCompare >::iterator |
◆ pointer
| typedef value_type* CppCommon::BinTree< T, TCompare >::pointer |
◆ reference
| typedef value_type& CppCommon::BinTree< T, TCompare >::reference |
◆ reverse_iterator
| typedef BinTreeReverseIterator<BinTree<T, TCompare>, T> CppCommon::BinTree< T, TCompare >::reverse_iterator |
◆ size_type
| typedef size_t CppCommon::BinTree< T, TCompare >::size_type |
◆ value_compare
| typedef TCompare CppCommon::BinTree< T, TCompare >::value_compare |
◆ value_type
| typedef T CppCommon::BinTree< T, TCompare >::value_type |
Constructor & Destructor Documentation
◆ BinTree() [1/4]
|
inlineexplicitnoexcept |
◆ BinTree() [2/4]
|
inlinenoexcept |
Definition at line 13 of file bintree.inl.
◆ BinTree() [3/4]
|
defaultnoexcept |
◆ BinTree() [4/4]
|
defaultnoexcept |
◆ ~BinTree()
|
defaultnoexcept |
Member Function Documentation
◆ begin() [1/2]
|
inlinenoexcept |
Definition at line 71 of file bintree.inl.
◆ begin() [2/2]
|
inlinenoexcept |
Get the begin binary tree iterator.
Definition at line 65 of file bintree.inl.
◆ cbegin()
|
inlinenoexcept |
Definition at line 77 of file bintree.inl.
◆ cend()
|
inlinenoexcept |
Definition at line 95 of file bintree.inl.
◆ clear()
|
inlinenoexcept |
Clear the binary tree.
Definition at line 399 of file bintree.inl.
◆ compare()
|
inlinenoexcept |
◆ crbegin()
|
inlinenoexcept |
Definition at line 113 of file bintree.inl.
◆ crend()
|
inlinenoexcept |
Definition at line 131 of file bintree.inl.
◆ empty()
|
inlinenoexcept |
◆ end() [1/2]
|
inlinenoexcept |
Definition at line 89 of file bintree.inl.
◆ end() [2/2]
|
inlinenoexcept |
Get the end binary tree iterator.
Definition at line 83 of file bintree.inl.
◆ erase() [1/2]
|
inlinenoexcept |
Erase the given item from the binary tree.
- Parameters
-
it - Iterator to the erased item
- Returns
- Erased item iterator
Definition at line 326 of file bintree.inl.
◆ erase() [2/2]
|
inlinenoexcept |
Erase the given item from the binary tree.
- Parameters
-
item - Item to erase
- Returns
- Erased item
Definition at line 320 of file bintree.inl.
◆ find() [1/2]
|
inlinenoexcept |
Definition at line 143 of file bintree.inl.
◆ find() [2/2]
|
inlinenoexcept |
Find the iterator which points to the first equal item in the binary tree or return end iterator.
Definition at line 137 of file bintree.inl.
◆ highest() [1/2]
|
inlinenoexcept |
Definition at line 49 of file bintree.inl.
◆ highest() [2/2]
|
inlinenoexcept |
Get the highest binary tree item.
Definition at line 43 of file bintree.inl.
◆ insert() [1/2]
|
inlinenoexcept |
Insert a new item into the binary tree with a position hint.
- Parameters
-
position - Iterator position to the inserted item item - Item to insert
- Returns
- Pair with the iterator to the inserted item and success flag
Definition at line 266 of file bintree.inl.
◆ insert() [2/2]
|
inlinenoexcept |
Insert a new item into the binary tree.
- Parameters
-
item - Item to insert
- Returns
- Pair with the iterator to the inserted item and success flag
- Examples
- containers_bintree.cpp.
Definition at line 260 of file bintree.inl.
◆ lower_bound() [1/2]
|
inlinenoexcept |
Definition at line 185 of file bintree.inl.
◆ lower_bound() [2/2]
|
inlinenoexcept |
Find the iterator which points to the first item that not less than the given item in the binary tree or return end iterator.
Definition at line 179 of file bintree.inl.
◆ lowest() [1/2]
|
inlinenoexcept |
Definition at line 27 of file bintree.inl.
◆ lowest() [2/2]
|
inlinenoexcept |
Get the lowest binary tree item.
Definition at line 21 of file bintree.inl.
◆ operator bool()
|
inlineexplicitnoexcept |
◆ operator=() [1/2]
|
defaultnoexcept |
◆ operator=() [2/2]
|
defaultnoexcept |
◆ rbegin() [1/2]
|
inlinenoexcept |
Definition at line 107 of file bintree.inl.
◆ rbegin() [2/2]
|
inlinenoexcept |
Get the reverse begin binary tree iterator.
Definition at line 101 of file bintree.inl.
◆ rend() [1/2]
|
inlinenoexcept |
Definition at line 125 of file bintree.inl.
◆ rend() [2/2]
|
inlinenoexcept |
Get the reverse end binary tree iterator.
Definition at line 119 of file bintree.inl.
◆ root() [1/2]
|
inlinenoexcept |
◆ root() [2/2]
|
inlinenoexcept |
◆ size()
|
inlinenoexcept |
◆ swap()
|
inlinenoexcept |
Swap two instances.
Definition at line 406 of file bintree.inl.
◆ upper_bound() [1/2]
|
inlinenoexcept |
Definition at line 229 of file bintree.inl.
◆ upper_bound() [2/2]
|
inlinenoexcept |
Find the iterator which points to the first item that greater than the given item in the binary tree or return end iterator.
Definition at line 223 of file bintree.inl.
Friends And Related Symbol Documentation
◆ swap
|
friend |
The documentation for this class was generated from the following files:
- include/containers/bintree.h
- include/containers/bintree.inl