Intrusive balanced Splay binary tree container. More...

#include <bintree_splay.h>

Classes
struct	Node
	Splay binary tree node. More...

Public Types
typedef T	value_type

typedef TCompare	value_compare

typedef value_type &	reference

typedef const value_type &	const_reference

typedef value_type *	pointer

typedef const value_type *	const_pointer

typedef ptrdiff_t	difference_type

typedef size_t	size_type

typedef BinTreeIterator< BinTreeSplay< T, TCompare >, T >	iterator

typedef BinTreeConstIterator< BinTreeSplay< T, TCompare >, T >	const_iterator

typedef BinTreeReverseIterator< BinTreeSplay< T, TCompare >, T >	reverse_iterator

typedef BinTreeConstReverseIterator< BinTreeSplay< T, TCompare >, T >	const_reverse_iterator

Public Member Functions
	BinTreeSplay (const TCompare &compare=TCompare()) noexcept

template<class InputIterator >
	BinTreeSplay (InputIterator first, InputIterator last, const TCompare &compare=TCompare()) noexcept

	BinTreeSplay (const BinTreeSplay &) noexcept=default

	BinTreeSplay (BinTreeSplay &&) noexcept=default

	~BinTreeSplay () noexcept=default

BinTreeSplay &	operator= (const BinTreeSplay &) noexcept=default

BinTreeSplay &	operator= (BinTreeSplay &&) noexcept=default

	operator bool () const noexcept
	Check if the binary tree is not empty. More...

bool	empty () const noexcept
	Is the binary tree empty? More...

size_t	size () const noexcept
	Get the binary tree size. More...

T *	root () noexcept
	Get the root binary tree item. More...

const T *	root () const noexcept

T *	lowest () noexcept
	Get the lowest binary tree item. More...

const T *	lowest () const noexcept

T *	highest () noexcept
	Get the highest binary tree item. More...

const T *	highest () const noexcept

bool	compare (const T &item1, const T &item2) const noexcept
	Compare two items: if the first item is less than the second one? More...

iterator	begin () noexcept
	Get the begin binary tree iterator. More...

const_iterator	begin () const noexcept

const_iterator	cbegin () const noexcept

iterator	end () noexcept
	Get the end binary tree iterator. More...

const_iterator	end () const noexcept

const_iterator	cend () const noexcept

reverse_iterator	rbegin () noexcept
	Get the reverse begin binary tree iterator. More...

const_reverse_iterator	rbegin () const noexcept

const_reverse_iterator	crbegin () const noexcept

reverse_iterator	rend () noexcept
	Get the reverse end binary tree iterator. More...

const_reverse_iterator	rend () const noexcept

const_reverse_iterator	crend () const noexcept

iterator	find (const T &item) noexcept
	Find the iterator which points to the first equal item in the binary tree or return end iterator. More...

const_iterator	find (const T &item) const noexcept

iterator	lower_bound (const T &item) noexcept
	Find the iterator which points to the first item that not less than the given item in the binary tree or return end iterator. More...

const_iterator	lower_bound (const T &item) const noexcept

iterator	upper_bound (const T &item) noexcept
	Find the iterator which points to the first item that greater than the given item in the binary tree or return end iterator. More...

const_iterator	upper_bound (const T &item) const noexcept

std::pair< iterator, bool >	insert (T &item) noexcept
	Insert a new item into the binary tree. More...

std::pair< iterator, bool >	insert (const const_iterator &position, T &item) noexcept
	Insert a new item into the binary tree with a position hint. More...

T *	erase (const T &item) noexcept
	Erase the given item from the binary tree. More...

iterator	erase (const iterator &it) noexcept
	Erase the given item from the binary tree. More...

void	clear () noexcept
	Clear the binary tree. More...

void	swap (BinTreeSplay &bintree) noexcept
	Swap two instances. More...

Friends
template<typename U , typename UCompare >
void	swap (BinTreeSplay< U, UCompare > &bintree1, BinTreeSplay< U, UCompare > &bintree2) noexcept

Detailed Description

template<typename T, typename TCompare = std::less<T>>
class CppCommon::BinTreeSplay< T, TCompare >

Intrusive balanced Splay binary tree container.

Not thread-safe.

Overview
A splay tree is a self-balancing binary search tree with the additional unusual property that recently accessed elements are quick to access again. It performs basic operations such as insertion, look-up and removal in O(log(n)) amortized time. For many non-uniform sequences of operations, splay trees perform better than other search trees, even when the specific pattern of the sequence is unknown. The splay tree was invented by Daniel Sleator and Robert Tarjan.

All normal operations on a binary search tree are combined with one basic operation, called splaying. Splaying the tree for a certain element rearranges the tree so that the element is placed at the root of the tree. One way to do this is to first perform a standard binary tree search for the element in question, and then use tree rotations in a specific fashion to bring the element to the top. Alternatively, a bottom-up algorithm can combine the search and the tree reorganization.

Advantages and disadvantages
Good performance for a splay tree depends on the fact that it is self- balancing, and indeed self optimising, in that frequently accessed nodes will move nearer to the root where they can be accessed more quickly. This is an advantage for nearly all practical applications, and is particularly useful for implementing caches; however it is important to note that for uniform access, a splay tree's performance will be considerably (although not asymptotically) worse than a somewhat balanced simple binary search tree.

Splay trees also have the advantage of being considerably simpler to implement than other self-balancing binary search trees, such as red- black trees or AVL trees, while their average-case performance is just as efficient. Also, splay trees do not need to store any bookkeeping data, thus minimizing memory requirements. However, these other data structures provide worst-case time guarantees, and can be more efficient in practice for uniform access.

One worst case issue with the basic splay tree algorithm is that of sequentially accessing all the elements of the tree in the sort order. This leaves the tree completely unbalanced (this takes n accesses - each an O(1) operation). Reaccessing the first item triggers an operation that takes O(n) operations to rebalance the tree before returning the first item. This is a significant delay for that final operation, although the amortised performance over the entire sequence is actually O(1). However, recent research shows that randomly rebalancing the tree can avoid this unbalancing effect and give similar performance to the other self- balancing algorithms.

It is possible to create a persistent version of splay trees which allows access to both the previous and new versions after an update. This requires amortized O(log n) space per update.

Contrarily to other types of self balancing trees, splay trees work well with nodes containing identical keys. Even with identical keys, performance remains amortized O(log n). All tree operations preserve the order of the identical nodes within the tree, which is a property similar to stable sorting algorithms. A carefully designed find operation can return the left most or right most node of a given key.

The splay operation
When a node x is accessed, a splay operation is performed on x to move it to the root. To perform a splay operation we carry out a sequence of splay steps, each of which moves x closer to the root. As long as x has a grandparent, each particular step depends on two factors:

Whether x is the left or right child of its parent node, p,
Whether p is the left or right child of its parent, g (the grandparent of x).

Thus, there are four cases when x has a grandparent. They fall into two types of splay steps.

Zig-zag step

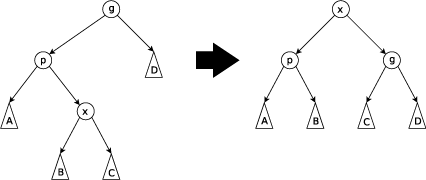
Zig-zag Step: One zig-zag case is when x is the right child of p and p is the left child of g (shown above). p is the new left child of x, g is the new right child of x, and the subtrees A, B, C, and D of x, p, and g are rearranged as necessary. The other zig-zag case is the mirror image of this, i.e. when x is the left child of p and p is the right child of g. Note that a zig-zag step is equivalent to doing a rotation on the edge between x and p, then doing a rotation on the edge between x and g.

Zig-zig step

Zig-zig Step: One zig-zig case is when x is the left child of p and p is the left child of g (shown above). p is the new right child of x, g is the new right child of p, and the subtrees A, B, C, and D of x, p, and g are rearranged as necessary. The other zig-zig case is the mirror image of this, i.e. when x is the right child of p and p is the right child of g. Note that zig-zig steps are the only thing that differentiate splay trees from the rotate to root method indroduced by Allen and Munro prior to the introduction of splay trees.

Zig step

Zig Step: There is also a third kind of splay step that is done when x has a parent p but no grandparent. This is called a zig step and is simply a rotation on the edge between x and p. Zig steps exist to deal with the parity issue and will be done only as the last step in a splay operation and only when x has odd depth at the beginning of the operation.

By performing a splay operation on the node of interest after every access, we keep recently accessed nodes near the root and keep the tree roughly balanced, so that we achieve the desired amortized time bounds.

Performance theorems
There are several theorems and conjectures regarding the worst-case runtime for performing a sequence S of m accesses in a splay tree containing n elements.

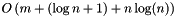
Balance Theorem: The cost of performing the sequence S is $O\left(m + (\log n + 1) + n\log(n) \right)$ . In other words, splay trees perform as well as static balanced binary search trees on sequences of at least n accesses.

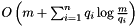
Static Optimality Theorem: Let qi be the number of times element i is accessed in S. The cost of performing S is $O\left(m+\sum_{i=1}^n q_i\log\frac{m}{q_i}\right)$ . In other words, splay trees perform as well as optimum static binary search trees on sequences of at least n accesses.

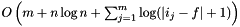
Static Finger Theorem: Let ij be the element accessed in the jth access of S and let f be any fixed element (the finger). The cost of performing S is $O\left(m+n\log n+\sum_{j=1}^m \log(|i_j-f|+1) \right)$ .

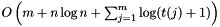
Working Set Theorem: Let t(j) be the number of distinct elements accessed between access j and the previous time element ij was accessed. The cost of performing S is $O\left(m+n\log n+\sum_{j=1}^m \log(t(j)+1) \right)$ .

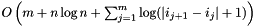
Dynamic Finger Theorem: The cost of performing S is $O\left(m+n\log n+\sum_{j=1}^m \log(|i_{j+1}-i_j|+1) \right)$ .

Scanning Theorem: Also known as the Sequential Access Theorem. Accessing the n elements of a splay tree in symmetric order takes O(n) time, regardles of the initial structure of the splay tree. The tightest upper bound proven so far is 4.5n.

Dynamic optimality conjecture
In addition to the proven performance guarantees for splay trees there is an unproven conjecture of great interest from the original Sleator and Tarjan paper. This conjecture is known as the dynamic optimality conjecture and it basically claims that splay trees perform as well as any other binary search tree algorithm up to a constant factor.

Dynamic Optimality Conjecture: Let A be any binary search tree algorithm that accesses an element x by traversing the path from the root to x at a cost of d(x) + 1, and that between accesses can make any rotations in the tree at a cost of 1 per rotation. Let A(S) be the cost for A to perform the sequence S of accesses. Then the cost for a splay tree to perform the same accesses is O(n + A(S)).

There is a special case of the dynamic optimality conjecture known as the traversal conjecture that is also unproven.

Traversal Conjecture: Let T1 and T2 be two splay trees containing the same elements. Let S be the sequence obtained by visiting the elements in T2 in preorder (i.e. depth first search order). The total cost of performing the sequence S of acesses on T1 is O(n).

Usage
Splay tree might be used in different caches and provides near O(1) lookup to the most frequent access items.

References

Sleator and R.E. Tarjan. Self-Adjusting Binary Search Trees. Journal of the ACM 32:3, pages 652-686, 1985.
R. Cole, B. Mishra, J. Schmidt, A. Siegel. On the Dynamic Finger Conjecture for Splay Trees. Part I: Splay Sorting log n-Block Sequences. SIAM Journal on Computing 30, pages 1-43, 2000.
R. Cole. On the Dynamic Finger Conjecture for Splay Trees. Part II: The Proof. SIAM Journal on Computing 30, pages 44-85, 2000.
R.E. Tarjan. Sequential access in splay trees takes linear time. Combinatorica 5, pages 367-378, 1985.
Amr Elmasry. On the sequential access theorem and deque conjecture for splay trees. Theor. Comput. Sci. 314(3), pages 459-466, 2004.

Taken from:
Splay tree from Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/Splay_tree

Definition at line 197 of file bintree_splay.h.

Member Typedef Documentation

◆ const_iterator

template<typename T , typename TCompare = std::less<T>>

typedef BinTreeConstIterator<BinTreeSplay<T, TCompare>, T> CppCommon::BinTreeSplay< T, TCompare >::const_iterator

Definition at line 210 of file bintree_splay.h.

◆ const_pointer

template<typename T , typename TCompare = std::less<T>>

typedef const value_type* CppCommon::BinTreeSplay< T, TCompare >::const_pointer

Definition at line 206 of file bintree_splay.h.

◆ const_reference

template<typename T , typename TCompare = std::less<T>>

typedef const value_type& CppCommon::BinTreeSplay< T, TCompare >::const_reference

Definition at line 204 of file bintree_splay.h.

◆ const_reverse_iterator

template<typename T , typename TCompare = std::less<T>>

typedef BinTreeConstReverseIterator<BinTreeSplay<T, TCompare>, T> CppCommon::BinTreeSplay< T, TCompare >::const_reverse_iterator

Definition at line 212 of file bintree_splay.h.

◆ difference_type

template<typename T , typename TCompare = std::less<T>>

typedef ptrdiff_t CppCommon::BinTreeSplay< T, TCompare >::difference_type

Definition at line 207 of file bintree_splay.h.

◆ iterator

template<typename T , typename TCompare = std::less<T>>

typedef BinTreeIterator<BinTreeSplay<T, TCompare>, T> CppCommon::BinTreeSplay< T, TCompare >::iterator

Definition at line 209 of file bintree_splay.h.

◆ pointer

template<typename T , typename TCompare = std::less<T>>

typedef value_type* CppCommon::BinTreeSplay< T, TCompare >::pointer

Definition at line 205 of file bintree_splay.h.

◆ reference

template<typename T , typename TCompare = std::less<T>>

typedef value_type& CppCommon::BinTreeSplay< T, TCompare >::reference

Definition at line 203 of file bintree_splay.h.

◆ reverse_iterator

template<typename T , typename TCompare = std::less<T>>

typedef BinTreeReverseIterator<BinTreeSplay<T, TCompare>, T> CppCommon::BinTreeSplay< T, TCompare >::reverse_iterator

Definition at line 211 of file bintree_splay.h.

◆ size_type

template<typename T , typename TCompare = std::less<T>>

typedef size_t CppCommon::BinTreeSplay< T, TCompare >::size_type

Definition at line 208 of file bintree_splay.h.

◆ value_compare

template<typename T , typename TCompare = std::less<T>>

typedef TCompare CppCommon::BinTreeSplay< T, TCompare >::value_compare

Definition at line 202 of file bintree_splay.h.

◆ value_type

template<typename T , typename TCompare = std::less<T>>

typedef T CppCommon::BinTreeSplay< T, TCompare >::value_type

Definition at line 201 of file bintree_splay.h.

Constructor & Destructor Documentation

◆ BinTreeSplay() [1/4]

template<typename T , typename TCompare = std::less<T>>

CppCommon::BinTreeSplay< T, TCompare >::BinTreeSplay ( const TCompare & compare = TCompare() )

inlineexplicitnoexcept

Definition at line 224 of file bintree_splay.h.

◆ BinTreeSplay() [2/4]

template<typename T , typename TCompare >

template<class InputIterator >

CppCommon::BinTreeSplay< T, TCompare >::BinTreeSplay	(	InputIterator	first,
		InputIterator	last,
		const TCompare &	compare = `TCompare()`
	)

inlinenoexcept

Definition at line 13 of file bintree_splay.inl.

◆ BinTreeSplay() [3/4]

template<typename T , typename TCompare = std::less<T>>

CppCommon::BinTreeSplay< T, TCompare >::BinTreeSplay ( const BinTreeSplay< T, TCompare > & )

defaultnoexcept

◆ BinTreeSplay() [4/4]

template<typename T , typename TCompare = std::less<T>>

CppCommon::BinTreeSplay< T, TCompare >::BinTreeSplay ( BinTreeSplay< T, TCompare > && )

defaultnoexcept

◆ ~BinTreeSplay()

template<typename T , typename TCompare = std::less<T>>

CppCommon::BinTreeSplay< T, TCompare >::~BinTreeSplay ( )

defaultnoexcept

Member Function Documentation

◆ begin() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::begin

inlinenoexcept

Definition at line 71 of file bintree_splay.inl.

◆ begin() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::iterator CppCommon::BinTreeSplay< T, TCompare >::begin

inlinenoexcept

Get the begin binary tree iterator.

Definition at line 65 of file bintree_splay.inl.

◆ cbegin()

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::cbegin

inlinenoexcept

Definition at line 77 of file bintree_splay.inl.

◆ cend()

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::cend

inlinenoexcept

Definition at line 95 of file bintree_splay.inl.

◆ clear()

template<typename T , typename TCompare >

void CppCommon::BinTreeSplay< T, TCompare >::clear

inlinenoexcept

Clear the binary tree.

Definition at line 567 of file bintree_splay.inl.

◆ compare()

template<typename T , typename TCompare = std::less<T>>

bool CppCommon::BinTreeSplay< T, TCompare >::compare	(	const T &	item1,
		const T &	item2
	)		const

inlinenoexcept

Compare two items: if the first item is less than the second one?

Definition at line 258 of file bintree_splay.h.

◆ crbegin()

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_reverse_iterator CppCommon::BinTreeSplay< T, TCompare >::crbegin

inlinenoexcept

Definition at line 113 of file bintree_splay.inl.

◆ crend()

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_reverse_iterator CppCommon::BinTreeSplay< T, TCompare >::crend

inlinenoexcept

Definition at line 131 of file bintree_splay.inl.

◆ empty()

template<typename T , typename TCompare = std::less<T>>

bool CppCommon::BinTreeSplay< T, TCompare >::empty ( ) const

inlinenoexcept

Is the binary tree empty?

Definition at line 242 of file bintree_splay.h.

◆ end() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::end

inlinenoexcept

Definition at line 89 of file bintree_splay.inl.

◆ end() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::iterator CppCommon::BinTreeSplay< T, TCompare >::end

inlinenoexcept

Get the end binary tree iterator.

Definition at line 83 of file bintree_splay.inl.

◆ erase() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::iterator CppCommon::BinTreeSplay< T, TCompare >::erase ( const iterator & it )

inlinenoexcept

Erase the given item from the binary tree.

Parameters

it	- Iterator to the erased item

Returns: Erased item iterator

Definition at line 336 of file bintree_splay.inl.

◆ erase() [2/2]

template<typename T , typename TCompare >

T * CppCommon::BinTreeSplay< T, TCompare >::erase ( const T & item )

inlinenoexcept

Erase the given item from the binary tree.

Parameters

item	- Item to erase

Returns: Erased item

Definition at line 330 of file bintree_splay.inl.

◆ find() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::find ( const T & item ) const

inlinenoexcept

Definition at line 143 of file bintree_splay.inl.

◆ find() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::iterator CppCommon::BinTreeSplay< T, TCompare >::find ( const T & item )

inlinenoexcept

Find the iterator which points to the first equal item in the binary tree or return end iterator.

Definition at line 137 of file bintree_splay.inl.

◆ highest() [1/2]

template<typename T , typename TCompare >

const T * CppCommon::BinTreeSplay< T, TCompare >::highest

inlinenoexcept

Definition at line 49 of file bintree_splay.inl.

◆ highest() [2/2]

template<typename T , typename TCompare >

T * CppCommon::BinTreeSplay< T, TCompare >::highest

inlinenoexcept

Get the highest binary tree item.

Definition at line 43 of file bintree_splay.inl.

◆ insert() [1/2]

template<typename T , typename TCompare >

std::pair< typename BinTreeSplay< T, TCompare >::iterator, bool > CppCommon::BinTreeSplay< T, TCompare >::insert	(	const const_iterator &	position,
		T &	item
	)

inlinenoexcept

Insert a new item into the binary tree with a position hint.

Parameters

position	- Iterator position to the inserted item
item	- Item to insert

Returns: Pair with the iterator to the inserted item and success flag

Definition at line 289 of file bintree_splay.inl.

◆ insert() [2/2]

template<typename T , typename TCompare >

std::pair< typename BinTreeSplay< T, TCompare >::iterator, bool > CppCommon::BinTreeSplay< T, TCompare >::insert ( T & item )

inlinenoexcept

Insert a new item into the binary tree.

Parameters

item	- Item to insert

Returns: Pair with the iterator to the inserted item and success flag

Definition at line 283 of file bintree_splay.inl.

◆ lower_bound() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::lower_bound ( const T & item ) const

inlinenoexcept

Definition at line 196 of file bintree_splay.inl.

◆ lower_bound() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::iterator CppCommon::BinTreeSplay< T, TCompare >::lower_bound ( const T & item )

inlinenoexcept

Find the iterator which points to the first item that not less than the given item in the binary tree or return end iterator.

Definition at line 190 of file bintree_splay.inl.

◆ lowest() [1/2]

template<typename T , typename TCompare >

const T * CppCommon::BinTreeSplay< T, TCompare >::lowest

inlinenoexcept

Definition at line 27 of file bintree_splay.inl.

◆ lowest() [2/2]

template<typename T , typename TCompare >

T * CppCommon::BinTreeSplay< T, TCompare >::lowest

inlinenoexcept

Get the lowest binary tree item.

Definition at line 21 of file bintree_splay.inl.

◆ operator bool()

template<typename T , typename TCompare = std::less<T>>

CppCommon::BinTreeSplay< T, TCompare >::operator bool ( ) const

inlineexplicitnoexcept

Check if the binary tree is not empty.

Definition at line 239 of file bintree_splay.h.

◆ operator=() [1/2]

template<typename T , typename TCompare = std::less<T>>

BinTreeSplay& CppCommon::BinTreeSplay< T, TCompare >::operator= ( BinTreeSplay< T, TCompare > && )

defaultnoexcept

◆ operator=() [2/2]

template<typename T , typename TCompare = std::less<T>>

BinTreeSplay& CppCommon::BinTreeSplay< T, TCompare >::operator= ( const BinTreeSplay< T, TCompare > & )

defaultnoexcept

◆ rbegin() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_reverse_iterator CppCommon::BinTreeSplay< T, TCompare >::rbegin

inlinenoexcept

Definition at line 107 of file bintree_splay.inl.

◆ rbegin() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::reverse_iterator CppCommon::BinTreeSplay< T, TCompare >::rbegin

inlinenoexcept

Get the reverse begin binary tree iterator.

Definition at line 101 of file bintree_splay.inl.

◆ rend() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_reverse_iterator CppCommon::BinTreeSplay< T, TCompare >::rend

inlinenoexcept

Definition at line 125 of file bintree_splay.inl.

◆ rend() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::reverse_iterator CppCommon::BinTreeSplay< T, TCompare >::rend

inlinenoexcept

Get the reverse end binary tree iterator.

Definition at line 119 of file bintree_splay.inl.

◆ root() [1/2]

template<typename T , typename TCompare = std::less<T>>

const T* CppCommon::BinTreeSplay< T, TCompare >::root ( ) const

inlinenoexcept

Definition at line 249 of file bintree_splay.h.

◆ root() [2/2]

template<typename T , typename TCompare = std::less<T>>

T* CppCommon::BinTreeSplay< T, TCompare >::root ( )

inlinenoexcept

Get the root binary tree item.

Definition at line 248 of file bintree_splay.h.

◆ size()

template<typename T , typename TCompare = std::less<T>>

size_t CppCommon::BinTreeSplay< T, TCompare >::size ( ) const

inlinenoexcept

Get the binary tree size.

Definition at line 245 of file bintree_splay.h.

◆ swap()

template<typename T , typename TCompare >

void CppCommon::BinTreeSplay< T, TCompare >::swap ( BinTreeSplay< T, TCompare > & bintree )

inlinenoexcept

Swap two instances.

Definition at line 574 of file bintree_splay.inl.

◆ upper_bound() [1/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::const_iterator CppCommon::BinTreeSplay< T, TCompare >::upper_bound ( const T & item ) const

inlinenoexcept

Definition at line 248 of file bintree_splay.inl.

◆ upper_bound() [2/2]

template<typename T , typename TCompare >

BinTreeSplay< T, TCompare >::iterator CppCommon::BinTreeSplay< T, TCompare >::upper_bound ( const T & item )

inlinenoexcept

Find the iterator which points to the first item that greater than the given item in the binary tree or return end iterator.

Definition at line 242 of file bintree_splay.inl.

Friends And Related Function Documentation

◆ swap

template<typename T , typename TCompare = std::less<T>>

template<typename U , typename UCompare >

void swap	(	BinTreeSplay< U, UCompare > &	bintree1,
		BinTreeSplay< U, UCompare > &	bintree2
	)

friend

The documentation for this class was generated from the following files:

include/containers/bintree_splay.h
include/containers/bintree_splay.inl

Classes

Public Types

Public Member Functions

Friends

Detailed Description

template<typename T, typename TCompare = std::less<T>> class CppCommon::BinTreeSplay< T, TCompare >

Member Typedef Documentation

◆ const_iterator

◆ const_pointer

◆ const_reference

◆ const_reverse_iterator

◆ difference_type

◆ iterator

◆ pointer

◆ reference

◆ reverse_iterator

◆ size_type

◆ value_compare

◆ value_type

Constructor & Destructor Documentation

◆ BinTreeSplay() [1/4]

◆ BinTreeSplay() [2/4]

◆ BinTreeSplay() [3/4]

◆ BinTreeSplay() [4/4]

◆ ~BinTreeSplay()

Member Function Documentation

◆ begin() [1/2]

◆ begin() [2/2]

◆ cbegin()

◆ cend()

◆ clear()

◆ compare()

◆ crbegin()

◆ crend()

◆ empty()

◆ end() [1/2]

◆ end() [2/2]

◆ erase() [1/2]

◆ erase() [2/2]

◆ find() [1/2]

◆ find() [2/2]

◆ highest() [1/2]

◆ highest() [2/2]

◆ insert() [1/2]

◆ insert() [2/2]

◆ lower_bound() [1/2]

◆ lower_bound() [2/2]

◆ lowest() [1/2]

◆ lowest() [2/2]

◆ operator bool()

◆ operator=() [1/2]

◆ operator=() [2/2]

◆ rbegin() [1/2]

◆ rbegin() [2/2]

◆ rend() [1/2]

◆ rend() [2/2]

◆ root() [1/2]

◆ root() [2/2]

◆ size()

◆ swap()

◆ upper_bound() [1/2]

◆ upper_bound() [2/2]

Friends And Related Function Documentation

◆ swap

template<typename T, typename TCompare = std::less<T>>
class CppCommon::BinTreeSplay< T, TCompare >